Tutorial 2: Introduction to NumPy and Pandas

Tutorial 2: Introduction to NumPy and Pandas#

One of the most used packages within our discipline are NumPy and Pandas. This tutorial will focus on teaching you the basics of both of them.

Note: This tutorial is heavily based upon the work of others

Important: This tutorial is not part of your final grade. You simply have to pass it by answering the questions.

Important before we start#

Make sure that you save this file before you continue, else you will lose everything. To do so, go to Bestand/File and click on Een kopie opslaan in Drive/Save a Copy on Drive!

Now, rename the file into Week1_Tutorial2.ipynb. You can do so by clicking on the name in the top of this screen.

Learning Objectives#

NumPy

Use NumPy to create arrays with built-in functions inlcuding np.array(), np.arange(), np.linspace() and np.full(), np.zeros(), np.ones()
Be able to access values from a NumPy array by numeric indexing, slicing, and boolean indexing
Perform mathematical operations on and with arrays.
Explain what broadcasting is and how to use it.
Reshape arrays by adding/removing/reshaping axes with .reshape(), np.newaxis(), .ravel(), .flatten()
Understand how to use built-in NumPy functions like np.sum(), np.mean(), np.log() as stand alone functions or as methods of numpy arrays (when available)

Pandas

Create Pandas series with pd.Series() and Pandas dataframe with pd.DataFrame()
Be able to access values from a Series/DataFrame by numeric indexing, slicing and boolean indexing using notation such as df[], df.loc[], df.iloc[], df.query[]
Perform basic arithmetic operations between two Pandas series and anticipate the result.
Describe how Pandas assigns dtypes to Series and what the object dtype is
Read a standard .csv file from a local path or url using Pandas pd.read_csv().
Explain the relationship and differences between np.ndarray, pd.Series and pd.DataFrame objects in Python.

Performing the exercise#

You will do so by performing the scripts in this Python Jupyter notebook. To run any script in the code-boxes below use crtl+enter. In some instances, it is necessary to make changes to particular pieces of code in the code-boxes. When this is the case, this will be asked to you before you arrive at the actual script. This is indicated by means of an Action. When a script is running this is indicated by the * on the left side of the window.

1. Introduction to Python Packages#

Packages are an essential building block in programming. Without packages, we’d spend lots of time writing code that’s already been written. Imagine having to write code from scratch every time you wanted to parse a file in a particular format. You’d never get anything done! That’s why we always want to use packages.

To understand Python packages, we’ll briefly need to look at scripts and modules. A script is something you execute in the shell to accomplish a defined task. To write a script, you’d type your code into your favorite text editor and save it with the .py extension. You can then use the python command in a terminal to execute your script.

A module on the other hand is a Python program that you import, either in interactive mode or into your other programs. “Module” is really an umbrella term for reusable code.

A Python package usually consists of several modules. Physically, a package is a folder containing modules and maybe other folders that themselves may contain more folders and modules. Conceptually, it’s a namespace. This simply means that a package’s modules are bound together by a package name, by which they may be referenced.

The packages we will use for this tutorial include:

OS is a python module that provides a portable way of using operating system dependent functionality i.e. manipulating paths

NumPy stands for “Numerical Python” and it is the standard Python library used for working with arrays (i.e., vectors & matrices), linear algerba, and other numerical computations. NumPy is written in C, making NumPy arrays faster and more memory efficient than Python lists or arrays

Pandas is most popular Python library for tabular data structures. You can think of Pandas as an extremely powerful version of Excel (but free and with a lot more features!)

Importing a package#

We’ll import a package using the import statement:

import <package>

2. Introduction to NumPy#

NumPy can be installed using pip (in google colab pandas and numpy packages are already installed, hence, we will skip this part):

!pip install numpy

3. NumPy Arrays#

What are Arrays?#

Arrays are “n-dimensional” data structures that can contain all the basic Python data types, e.g., floats, integers, strings etc, but work best with numeric data. NumPy arrays (“ndarrays”) are homogenous, which means that items in the array should be of the same type. ndarrays are also compatible with numpy’s vast collection of in-built functions!

Usually we import numpy with the alias np (to avoid having to type out n-u-m-p-y every time we want to use it):

import numpy as np

A numpy array is sort of like a list:

np.full((5, 5), 1)

array([[1, 1, 1, 1, 1],
       [1, 1, 1, 1, 1],
       [1, 1, 1, 1, 1],
       [1, 1, 1, 1, 1],
       [1, 1, 1, 1, 1]])

np.arange(1,21)

array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17,
       18, 19, 20])

my_list = [1, 2, 3, 4, 5]
my_list

my_array = np.array([1, 2, 3, 4, 5])
my_array

But it has the type ndarray:

type(my_array)

Unlike a list, arrays can only hold a single type (usually numbers):

my_list = [1, "hi"]
my_list

my_array = np.array((1, "hi"))
my_array

Above: NumPy converted the integer 1 into the string '1'!

Creating arrays#

ndarrays are typically created using two main methods:

From existing data (usually lists or tuples) using np.array(), like we saw above; or,
Using built-in functions such as np.arange(), np.linspace(), np.zeros(), etc.

my_list = [1, 2, 3]
np.array(my_list)

Just like you can have “multi-dimensional lists” (by nesting lists in lists), you can have multi-dimensional arrays (indicated by double square brackets [[ ]]):

list_2d = [[1, 2], [3, 4], [5, 6]]
list_2d

array_2d = np.array(list_2d)
array_2d

You’ll probably use the built-in numpy array creators quite often. Here are some common ones (hint - don’t forget to check the docstrings for help with these functions, if you’re in Jupyter, remeber the shift + tab shortcut):

np.arange(1, 5)  # from 1 inclusive to 5 exclusive. The counting always starts from 0 and not 1

np.arange(0, 11, 2)  # step by 2 from 1 to 11

np.linspace(0, 10, 5)  # 5 equally spaced points between 0 and 10

np.ones((2, 2))  # an array of ones with size 2 x 2. Always starts with the row then column

np.zeros((2, 3))  # an array of zeros with size 2 x 3

np.full((3, 3), 3.14)  # an array of the number 3.14 with size 3 x 3

np.full((3, 3, 3), 3.14)  # an array of the number 3.14 with size 3 x 3 x 3

np.random.rand(5, 2)  # random numbers uniformly distributed from 0 to 1 with size 5 x 2

There are many useful attributes/methods that can be called off numpy arrays:

print(dir(np.ndarray))

x = np.random.rand(5, 2)
x

x.transpose() # converts the rows to columns and vice versa

x.mean()

x.astype(int) # truncates to the nearest whole number

Array Shapes#

As you just saw above, arrays can be of any dimension, shape and size you desire. In fact, there are three main array attributes you need to know to work out the characteristics of an array:

.ndim: the number of dimensions of an array
.shape: the number of elements in each dimension (like calling len() on each dimension)
.size: the total number of elements in an array (i.e., the product of .shape) Python f-string is an amazing way to format strings by including a code within the string as shown below

array_1d = np.ones(3)
print(f"Dimensions: {array_1d.ndim}")
print(f"     Shape: {array_1d.shape}")
print(f"      Size: {array_1d.size}")

Let’s turn that print action into a function and try out some other arrays:

def print_array(x):
    print(f"Dimensions: {x.ndim}")
    print(f"     Shape: {x.shape}")
    print(f"      Size: {x.size}")
    print("")
    print(x)

array_2d = np.ones((3, 2))
print_array(array_2d)

array_4d = np.ones((1, 2, 3, 4))
print_array(array_4d)

After 3 dimensions, printing arrays starts getting pretty messy. As you can see above, the number of square brackets ([ ]) in the printed output indicate how many dimensions there are: for example, above, the output starts with 4 square brackets [[[[ indicative of a 4D array.

1-d Arrays#

One of the most confusing things about numpy is 1-d arrays (vectors) can have 3 possible shapes!

x = np.ones(5)
print_array(x)

y = np.ones((1, 5))
print_array(y)

z = np.ones((5, 1))
print_array(z)

We can use np.array_equal() to determine if two arrays have the same shape and elements:

np.array_equal(x, x)

np.array_equal(x, y)

np.array_equal(x, z)

np.array_equal(y, z)

The shape of your 1-d arrays can actually have big implications on your mathematical operations!

print(f"x: {x}")
print(f"y: {y}")
print(f"z: {z}")

x + y  # makes sense

y + z  # wait, what?

What happened in the cell above is “broadcasting” and we’ll discuss it below.

4. Array Operations and Broadcasting#

Elementwise operations#

Elementwise operations refer to operations applied to each element of an array or between the paired elements of two arrays.

x = np.ones(4)
x

y = x + 1
y

x - y # subtraction

x == y # compares the two arrays

x * y # multiplication 

x ** y #exponentiation operator or in simpler terms the power operator

x / y #division

np.array_equal(x, y)

Broadcasting#

ndarrays with different sizes cannot be directly used in arithmetic operations:

a = np.ones((2, 2))
b = np.ones((3, 3))
a + b # this produces an error cause of the different sizes of the arrays

Broadcasting describes how NumPy treats arrays with different shapes during arithmetic operations. The idea is to wrangle data so that operations can occur element-wise.

Let’s see an example. Say I sell pies on my weekends. I sell 3 types of pies at different prices, and I sold the following number of each pie last weekend. I want to know how much money I made per pie type per day.

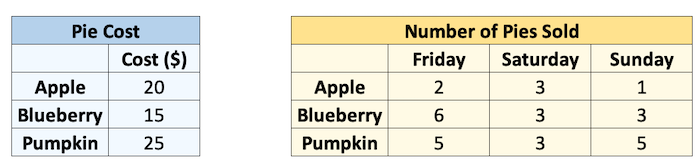
cost = np.array([20, 15, 25])
print("Pie cost:")
print(cost)
sales = np.array([[2, 3, 1], [6, 3, 3], [5, 3, 5]])
print("\nPie sales (#):")
print(sales)

How can we multiply these two arrays together? We could use a loop:

total = np.zeros((3, 3))  # initialize an array of 0's
for col in range(sales.shape[1]):
    total[:, col] = sales[:, col] * cost
total

Or we could make them the same size, and multiply corresponding elements “elementwise”:

cost = np.repeat(cost, 3).reshape((3, 3))
cost

cost * sales

Broadcasting is just Numpy essentially doing the np.repeat() for you under the hood:

cost = np.array([20, 15, 25]).reshape(3, 1)
print(f" cost shape: {cost.shape}")
sales = np.array([[2, 3, 1], [6, 3, 3], [5, 3, 5]])
print(f"sales shape: {sales.shape}")

sales * cost

In NumPy the smaller array is “broadcast” across the larger array so that they have compatible shapes:

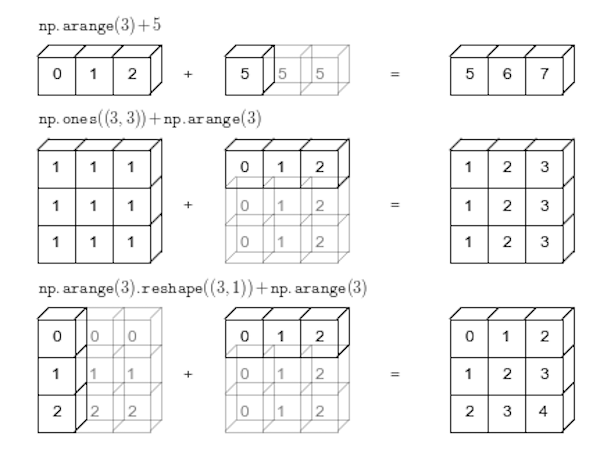
Source: Python Data Science Handbook by Jake VanderPlas (2016)

Why should you care about broadcasting? Well, it’s cleaner and faster than looping and it also affects the array shapes resulting from arithmetic operations. Below, we can time how long it takes to loop vs broadcast:

cost = np.array([20, 15, 25]).reshape(3, 1)
sales = np.array([[2, 3, 1],
                  [6, 3, 3],
                  [5, 3, 5]])
total = np.zeros((3, 3))

time_loop = %timeit -q -o -r 3 for col in range(sales.shape[1]): total[:, col] = sales[:, col] * np.squeeze(cost)
time_vec = %timeit -q -o -r 3 cost * sales
print(f"Broadcasting is {time_loop.average / time_vec.average:.2f}x faster than looping here.")

Of course, not all arrays are compatible! NumPy compares arrays element-wise. It starts with the trailing dimensions, and works its way forward. Dimensions are compatible if:

they are equal, or
one of them is 1.

Use the code below to test out array compatibitlity:

a = np.ones((3, 2))
b = np.ones((3, 2, 1))
print(f"The shape of a is: {a.shape}")
print(f"The shape of b is: {b.shape}")
print("")
try:
    print(f"The shape of a + b is: {(a + b).shape}")
except:
    print(f"ERROR: arrays are NOT broadcast compatible!")

Reshaping Arrays#

There are 3 key reshaping methods I want you to know about for reshaping numpy arrays:

.reshape()
np.newaxis
.ravel()/.flatten()

x = np.full((4, 3), 3.14)
x

You’ll reshape arrays fairly often and the .reshape() method is pretty intuitive:

x.reshape(6, 2)

x.reshape(2, -1)  # using -1 will calculate the dimension for you (if possible)

a = np.ones(3)
print_array(a)
b = np.ones((3, 2))
print_array(b)

If I want to add these two arrays I won’t be able to because their dimensions are not compatible:

a + b

Sometimes you’ll want to add dimensions to an array for broadcasting purposes like this. We can do that with np.newaxis (note that None is an alias for np.newaxis). We can add a dimension to a to make the arrays compatible:

print_array(a[:, np.newaxis])  # same as a[:, None]

a[:, np.newaxis] + b

Finally, sometimes you’ll want to “flatten” arrays to a single dimension using .ravel() or .flatten(). .flatten() used to return a copy and .ravel() a view/reference but now they both return a copy so I can’t think of an important reason to use one over the other 🤷‍♂️

print_array(x.flatten())

print_array(x.ravel())

5. Indexing and slicing#

Concepts of indexing should be pretty familiar by now. Indexing arrays is similar to indexing lists but there are just more dimensions.

Numeric Indexing#

x = np.arange(10)
x

x[3]

x[2:]

x[:4]

x[2:5]

x[2:3]

x[-1]

x[-2]

x[5:0:-1] # the -1 means going backwards

For 2D arrays:

x = np.random.randint(10, size=(4, 6))
x

x[3, 4]  # do this

x[3][4]  # i do not like this as much

x[3]

len(x)  # generally, just confusing

x.shape

x[:, 2]  # column number 2

x[2:, :3]

x.T

x[1, 1] = 555555
x

z = np.zeros(5)
z

z[0] = 5
z

Boolean Indexing#

x = np.random.rand(10)
x

x + 1

x_thresh = x > 0.5
x_thresh

x[x_thresh] = 0.5  # set all elements  > 0.5 to be equal to 0.5
x

x = np.random.rand(10)
x

x[x > 0.5] = 0.5
x

6. More Useful NumPy Functions#

Numpy has many built-in functions for mathematical operations, really it has almost every numerical operation you might want to do in its library. I’m not going to explore the whole library here, but as an example of some of the available functions, consider working out the hypotenuse of a triangle that with sides 3m and 4m:

sides = np.array([3, 4])

There are several ways we could solve this problem. We could directly use Pythagoras’s Theorem:

$$c = \sqrt{a^2+b^2}$$

np.sqrt(np.sum([np.power(sides[0], 2), np.power(sides[1], 2)]))

We can leverage the fact that we’re dealing with a numpy array and apply a “vectorized” operation (more on that in a bit) to the whole vector at one time:

(sides ** 2).sum() ** 0.5

Or we can simply use a numpy built-in function (if it exists):

np.linalg.norm(sides)  

np.hypot(*sides)

Vectorization#

Broadly speaking, “vectorization” in NumPy refers to the use of optmized C code to perform an operation. Long-story-short, because numpy arrays are homogenous (contain the same dtype), we don’t need to check that we can perform an operation on elements of a sequence before we do the operation which results in a huge speed-up. You can kind of think of this concept as NumPy being able to perform an operation on the whole array at the same time rather than one-by-one (this is not actually the case, a super-efficient C loop is still running under the hood, but that’s an irrelevant detail). You can read more about vectorization here but all you need to know is that most operations in NumPy are vectorized, so just try to do things at an “array-level” rather than an “element-level”, e.g.:

# DONT DO THIS
array = np.array(range(5))
for i, element in enumerate(array):
    array[i] = element ** 2
array

# DO THIS
array = np.array(range(5))
array **= 2 

Let’s do a quick timing experiment:

# loop method
array = np.array(range(5))
time_loop = %timeit -q -o -r 3 for i, element in enumerate(array): array[i] = element ** 2
# vectorized method
array = np.array(range(5))
time_vec = %timeit -q -o -r 3 array ** 2
print(f"Vectorized operation is {time_loop.average / time_vec.average:.2f}x faster than looping here.")

7. Introduction to Pandas#

Pandas can be installed using pip:

!pip install pandas

We usually import pandas with the alias pd. You’ll see these two imports at the top of most data science workflows:

import pandas as pd

8. Pandas Series#

What are Series?#

A Series is like a NumPy array but with labels. They are strictly 1-dimensional and can contain any data type (integers, strings, floats, objects, etc), including a mix of them. Series can be created from a scalar, a list, ndarray or dictionary using pd.Series() (note the captial “S”). Here are some example series:

Creating Series#

By default, series are labelled with indices starting from 0. For example:

pd.Series(data = [-5, 1.3, 21, 6, 3])

But you can add a custom index:

pd.Series(data = [-5, 1.3, 21, 6, 3],
          index = ['a', 'b', 'c', 'd', 'e'])

You can create a Series from a dictionary:

pd.Series(data = {'a': 10, 'b': 20, 'c': 30})

Or from an ndarray:

pd.Series(data = np.random.randn(3))

Or even a scalar:

pd.Series(3.141)

pd.Series(data=3.141, index=['a', 'b', 'c'])

Series Characteristics#

Series can be given a name attribute. I almost never use this but it might come up sometimes:

s = pd.Series(data = np.random.randn(5), name='random_series')
s

s.name

s.rename("another_name")

You can access the index labels of your series using the .index attribute:

s.index

You can access the underlying data array using .to_numpy():

s.to_numpy()

pd.Series([[1, 2, 3], "b", 1]).to_numpy()

Indexing and Slicing Series#

Series are very much like ndarrays (in fact, series can be passed to most NumPy functions!). They can be indexed using square brackets [ ] and sliced using colon : notation:

s = pd.Series(data = range(5),
              index = ['A', 'B', 'C', 'D', 'E'])
s

s[0]

s[[1, 2, 3]]

s[0:3]

Note above how array-based indexing and slicing also returns the series index.

Series are also like dictionaries, in that we can access values using index labels:

s["A"]

s[["B", "D", "C"]]

s["A":"C"]

"A" in s

"Z" in s

Series do allow for non-unique indexing, but be careful because indexing operations won’t return unique values:

x = pd.Series(data = range(5),
              index = ["A", "A", "A", "B", "C"])
x

x["A"]

Finally, we can also do boolean indexing with series:

s[s >= 1]

s[s > s.mean()]

(s != 1)

Series Operations#

Unlike ndarrays operations between Series (+, -, /, *) align values based on their LABELS (not their position in the structure). The resulting index will be the sorted union of the two indexes. This gives you the flexibility to run operations on series regardless of their labels.

s1 = pd.Series(data = range(4),
               index = ["A", "B", "C", "D"])
s1

s2 = pd.Series(data = range(10, 14),
               index = ["B", "C", "D", "E"])
s2

s1 + s2

As you can see above, indices that match will be operated on. Indices that don’t match will appear in the product but with NaN values:

We can also perform standard operations on a series, like multiplying or squaring. NumPy also accepts series as an argument to most functions because series are built off numpy arrays (more on that later):

s1 ** 2

np.exp(s1)

Finally, just like arrays, series have many built-in methods for various operations. You can find them all by running help(pd.Series):

print([_ for _ in dir(pd.Series) if not _.startswith("_")])  # print all common methods

s1

s1.mean()

s1.sum()

s1.astype(float)

“Chaining” operations together is also common with pandas:

s1.add(3.141).astype(int).pow(2).mean()

Data Types#

Series can hold all the data types (dtypes) you’re used to, e.g., int, float, bool, etc. There are a few other special data types too (object, DateTime and Categorical) which we’ll talk about in this and later chapters. You can always read more about pandas dtypes in the documentation too. For example, here’s a series of dtype int64:

x = pd.Series(range(5))
x.dtype

The dtype “object” is used for series of strings or mixed data. Pandas is currently experimenting with a dedicated string dtype StringDtype, but it is still in testing.

x = pd.Series(['A', 'B'])
x

x = pd.Series(['A', 1, ["I", "AM", "A", "LIST"]])
x

While flexible, it is recommended to avoid the use of object dtypes because of higher memory requirements. Essentially, in an object dtype series, every single element stores information about its individual dtype. We can inspect the dtypes of all the elements in a mixed series in several ways, below I’ll use the map method:

x.map(type)

We can see that each object in our series has a different dtype. This comes at a cost. Compare the memory usage of the series below:

x1 = pd.Series([1, 2, 3])
print(f"x1 dtype: {x1.dtype}")
print(f"x1 memory usage: {x1.memory_usage(deep=True)} bytes")
print("")
x2 = pd.Series([1, 2, "3"])
print(f"x2 dtype: {x2.dtype}")
print(f"x2 memory usage: {x2.memory_usage(deep=True)} bytes")
print("")
x3 = pd.Series([1, 2, "3"]).astype('int8')  # coerce the object series to int8
print(f"x3 dtype: {x3.dtype}")
print(f"x3 memory usage: {x3.memory_usage(deep=True)} bytes")

In summary, try to use uniform dtypes where possible - they are more memory efficient!

One more gotcha, NaN (frequently used to represent missing values in data) is a float:

type(np.NaN)

This can be problematic if you have a series of integers and one missing value, because Pandas will cast the whole series to a float:

pd.Series([1, 2, 3, np.NaN])

Only recently, Pandas has implemented a “nullable integer dtype”, which can handle NaN in an integer series without affecting the dtype. Note the captial “I” in the type below, differentiating it from numpy’s int64 dtype:

pd.Series([1, 2, 3, np.NaN]).astype('Int64')

This is not the default in Pandas yet and functionality of this new feature is still subject to change.

9. Pandas DataFrames#

What are DataFrames?#

Pandas DataFrames are you’re new best friend. They are like the Excel spreadsheets you may be used to. DataFrames are really just Series stuck together! Think of a DataFrame as a dictionary of series, with the “keys” being the column labels and the “values” being the series data:

Creating DataFrames#

Dataframes can be created using pd.DataFrame() (note the capital “D” and “F”). Like series, index and column labels of dataframes are labelled starting from 0 by default:

pd.DataFrame([[1, 2, 3],
              [4, 5, 6],
              [7, 8, 9]])

We can use the index and columns arguments to give them labels:

pd.DataFrame([[1, 2, 3],
              [4, 5, 6],
              [7, 8, 9]],
             index = ["R1", "R2", "R3"],
             columns = ["C1", "C2", "C3"])

There are so many ways to create dataframes. I most often create them from dictionaries or ndarrays:

pd.DataFrame({"C1": [1, 2, 3],
              "C2": ['A', 'B', 'C']},
             index=["R1", "R2", "R3"])

pd.DataFrame(np.random.randn(5, 5),
             index=[f"row_{_}" for _ in range(1, 6)],
             columns=[f"col_{_}" for _ in range(1, 6)])

pd.DataFrame(np.array([['Tom', 7], ['Mike', 15], ['Tiffany', 3]]))

Here’s a table of the main ways you can create dataframes (see the Pandas documentation for more):

Create DataFrame from	Code
Lists of lists	`pd.DataFrame([['Tom', 7], ['Mike', 15], ['Tiffany', 3]])`
ndarray	`pd.DataFrame(np.array([['Tom', 7], ['Mike', 15], ['Tiffany', 3]]))`
Dictionary	`pd.DataFrame({"Name": ['Tom', 'Mike', 'Tiffany'], "Number": [7, 15, 3]})`
List of tuples	`pd.DataFrame(zip(['Tom', 'Mike', 'Tiffany'], [7, 15, 3]))`
Series	`pd.DataFrame({"Name": pd.Series(['Tom', 'Mike', 'Tiffany']), "Number": pd.Series([7, 15, 3])})`

Indexing and Slicing DataFrames#

There are several main ways to select data from a DataFrame:

[]
.loc[]
.iloc[]
Boolean indexing
.query()

df = pd.DataFrame({"Name": ["Tom", "Mike", "Tiffany"],
                   "Language": ["Python", "Python", "R"],
                   "Courses": [5, 4, 7]})
df

Indexing with `[]`#

Select columns by single labels, lists of labels, or slices:

df['Name']  # returns a series

df[['Name']]  # returns a dataframe!

df[['Name', 'Language']]

You can only index rows by using slices, not single values (but not recommended, see preferred methods below).

df[0] # doesn't work

df[0:1] # does work

df[1:] # does work

Indexing with `.loc` and `.iloc`#

Pandas created the methods .loc[] and .iloc[] as more flexible alternatives for accessing data from a dataframe. Use df.iloc[] for indexing with integers and df.loc[] for indexing with labels. These are typically the recommended methods of indexing in Pandas.

df

First we’ll try out .iloc which accepts integers as references to rows/columns:

df.iloc[0]  # returns a series

df.iloc[0:2]  # slicing returns a dataframe

df.iloc[2, 1]  # returns the indexed object

df.iloc[[0, 1], [1, 2]]  # returns a dataframe

Now let’s look at .loc which accepts labels as references to rows/columns:

df.loc[:, 'Name']

df.loc[:, 'Name':'Language']

df.loc[[0, 2], ['Language']]

Sometimes we want to use a mix of integers and labels to reference data in a dataframe. The easiest way to do this is to use .loc[] with a label then use an integer in combinations with .index or .columns:

df.index

df.columns

df.loc[df.index[0], 'Courses']  # I want to reference the first row and the column named "Courses"

df.loc[2, df.columns[1]]  # I want to reference row "2" and the second column

Boolean indexing#

Just like with series, we can select data based on boolean masks:

df

df[df['Courses'] > 5]

df[df['Name'] == "Tom"]

Indexing with `.query()`#

Boolean masks work fine, but I prefer to use the .query() method for selecting data. df.query() is a powerful tool for filtering data. It has an odd syntax, one of the strangest I’ve seen in Python, it is more like SQL - df.query() accepts a string expression to evaluate and it “knows” the names of the columns in your dataframe.

df.query("Courses > 4 & Language == 'Python'")

Note the use of single quotes AND double quotes above, lucky we have both in Python! Compare this to the equivalent boolean indexing operation and you can see that .query() is much more readable, especially as the query gets bigger!

df[(df['Courses'] > 4) & (df['Language'] == 'Python')]

Query also allows you to reference variable in the current workspace using the @ symbol:

course_threshold = 4
df.query("Courses > @course_threshold")

Indexing cheatsheet#

Method	Syntax	Output
Select column	`df[col_label]`	Series
Select row slice	`df[row_1_int:row_2_int]`	DataFrame
Select row/column by label	`df.loc[row_label(s), col_label(s)]`	Object for single selection, Series for one row/column, otherwise DataFrame
Select row/column by integer	`df.iloc[row_int(s), col_int(s)]`	Object for single selection, Series for one row/column, otherwise DataFrame
Select by row integer & column label	`df.loc[df.index[row_int], col_label]`	Object for single selection, Series for one row/column, otherwise DataFrame
Select by row label & column integer	`df.loc[row_label, df.columns[col_int]]`	Object for single selection, Series for one row/column, otherwise DataFrame
Select by boolean	`df[bool_vec]`	Object for single selection, Series for one row/column, otherwise DataFrame
Select by boolean expression	`df.query("expression")`	Object for single selection, Series for one row/column, otherwise DataFrame

Reading/Writing Data From External Sources#

.csv files#

A lot of the time you will be loading .csv files for use in pandas. You can use the pd.read_csv() function for this. We’ll use a real dataset of weather variables summarized by CORGIS Dataset Project from National Oceanic and Atmospheric Administration, the National Weather Service daily weather reports. There are so many arguments that can be used to help read in your .csv file in an efficient and appropriate manner, feel free to check them out now (by using shift + tab in Jupyter, or typing help(pd.read_csv)).

Pandas facilitates reading directly from a url - pd.read_csv() accepts urls as input:

path = 'https://github.com/ElcoK/BigData_AED/raw/main/week1/weather.csv'
df = pd.read_csv(path, index_col=0, parse_dates=True)
df

You can print a dataframe to .csv using df.to_csv(). Be sure to check out all of the possible arguments to write your dataframe exactly how you want it.

Other#

Pandas can read data from all sorts of other file types including HTML, JSON, Excel, Parquet, Feather, etc. There are generally dedicated functions for reading these file types, see the Pandas documentation here.

Common DataFrame Operations#

DataFrames have built-in functions for performing most common operations, e.g., .min(), idxmin(), sort_values(), etc. They’re all documented in the Pandas documentation here but I’ll demonstrate a few below:

df = pd.read_csv(path)
df.head()

df.columns # to view all the columns within the dataframe

df.min()

df['Data.Temperature.Avg Temp'].min()

df['Data.Temperature.Avg Temp'].idxmin() # position index of the min temperature

df.iloc[20]

df.sum()

Some methods like .mean() will only operate on numeric columns:

df.mean()

Some methods require arguments to be specified, like .sort_values():

df.sort_values(by='Data.Temperature.Max Temp')

df.sort_values(by='Data.Temperature.Max Temp', ascending=False).head()

Some methods will operate on the index/columns, like .sort_index():

df.sort_index(ascending=False)

10. Why ndarrays and Series and DataFrames?#

At this point, you might be asking why we need all these different data structures. Well, they all serve different purposes and are suited to different tasks. For example:

NumPy is typically faster/uses less memory than Pandas;
not all Python packages are compatible with NumPy & Pandas;
the ability to add labels to data can be useful (e.g., for time series);
NumPy and Pandas have different built-in functions available.

My advice: use the simplest data structure that fulfills your needs!

Finally, we’ve seen how to go from: ndarray (np.array()) -> series (pd.series()) -> dataframe (pd.DataFrame()). Remember that we can also go the other way: dataframe/series -> ndarray using df.to_numpy().